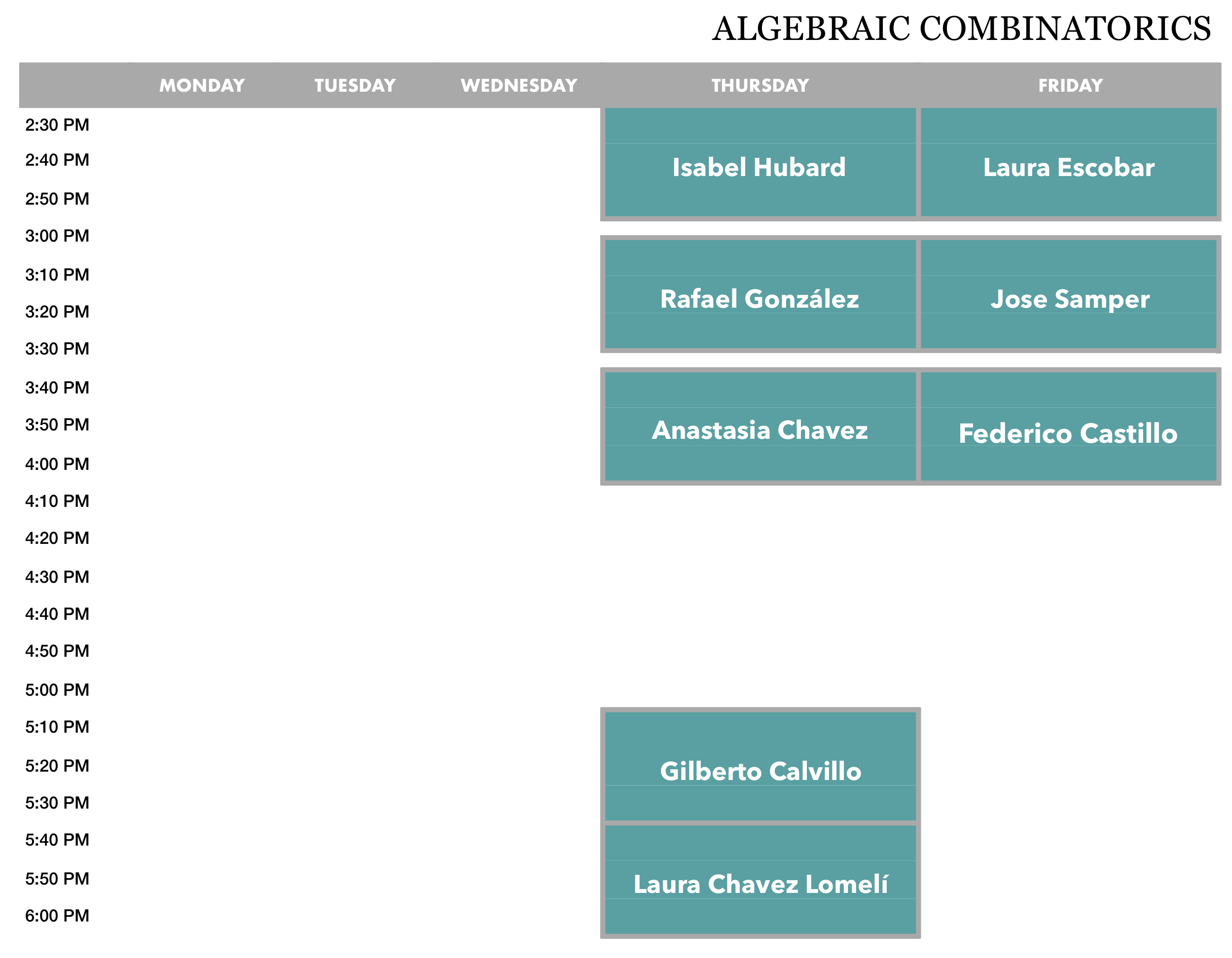
Session on Algebraic Combinatorics:
Thursday, August 8
14.30-15.00
Isabel Hubard (UNAM, México)
Abstract polytopes and their groups
In this talk the concept of an abstract polytopes will be introduced and we will talk about the two groups that encapsule all the information of the combinatorial structure.
15.05-15.35
Rafael González (Universidad Sergio Arboleda, Colombia)
A weighted generalization of the bond lattice of a graph
For any pair of positive integers n and k, we introduce a family of posets that generalize both the bond lattice of a graph and the poset of weighted partitions introduced by Dotsenko and Khoroshkin in the case $k=2$ of the complete graph, which was extended and studied by González D'León and Wachs. We show that for chordal graphs, these posets are EL-shellable and hence Cohen-Macaulay. The Möbius values of the máximal intervals induce an interesting family of symmetric functions that conjecturally distinguish trees. In the case of path graphs, the family of symmetric functions coincides with Garcia-Haiman's parking function symmetric functions. In the case k=2 of a tree, the symmetric function conjecturally contains the information of the h-vectors of graph associahedra studied by Postnikov, Reiner and Williams, and others. This is joint work with Michelle Wachs.
15.40-16.10
Anastasia Chavez (UC Davis, USA)
Characterizing quotients of positroids
We characterize quotients of specific families of positroids. Positroids are a special class of representable matroids introduced by Postnikov in the study of the nonnegative part of the Grassmannian. Postnikov defined several combinatorial objects that index positroids. In this talk, we make use of two of these objects to combinatorially characterize when certain positroids are quotients. Furthermore, we conjecture a general rule for quotients among arbitrary positroids on the same ground set.
17.10-17.40
Gilberto Calvillo (UNAM, México)
A geometrical characterization of matroids
It is well known that there are plenty of ways to characterize matroids. Some time ago I found one in pure geometric terms. The characterization is valid for integer polimatroids too. The idea arose from the realm of combinatorial optimization, so I will describe a geometrical property that is related to polytopes of polynomially solvable problems and then a stronger version for matroids that happens to characterize them.
17.45-18.15
Laura Chavez Lomelí ((UAM Azcapotzalco, México)
Balance en matroides
En 1976, A. Hoffman publicó un artículo en el que presenta un resultado sobre matrices totalmente unimodulares y una lista de aplicaciones de este a varios campos, incluyendo teoríaa de gríaficas. En el caso de gráficas, dicho resultado relaciona una noción de balance en cortes de aristas con el problema de flujo en redes. Dualmente el resultado se puede aplicar a circuitos obteniendo una versión de número cromático. El ``Lema de Hoffman", como se le conoce ahora, es (claramente) válido para matroides regulares y es natural tratar de extender estos conceptos y resultados a otras clases de matroides. En esta plática presentaremos algunos de los resultados nacidos de este estudio.
In 1976, A. Hoffman published a paper where he introduces a result on totally unimodular matrices along with a list of applications to various areas of science, among them, graph theory. For graphs, this result connects a notion of balance of edge cuts to network flows. Dually, it can be applied to circuits resulting on a version of chromatic number. ``Hoffman's Lemma" as it is now known, is (clearly) valid form regular matroids and it is natural to try to extend these concepts and results to other classes of matroids.In this talk we present some of the results derived from this study.
Friday, August 9
14.30-15.00
Laura Escobar (Washington University in St. Louis, USA)
Wall-crossing phenomena for Newton-Okounkov bodies
A Newton-Okounkov body is a convex set associated to a projective variety, equipped with a valuation. These bodies generalize the theory of Newton polytopes. Work of Kaveh-Manon gives an explicit link between tropical geometry and Newton-Okounkov bodies. We use this link to describe a wall-crossing phenomenon for Newton-Okounkov bodies. As an application we show how the wall-crossing formula for the tropicalization of $Gr(2, n)$ is an instance of our phenomenon for Newton-Okounkov bodies. This is joint work with Megumi Harada.
15.05-15.35
Jose Samper (MPIM-Bonn, Germany)
Monoides de Hopf y clases quasi-matroidales
Continuando con el trabajo de M. Aguiar y F. Ardila sobre monoides de Hopf y matroides, construimos un monoide que considera matroides al tiempo que un orden lineal sobre el conjunto base. Una de las ventajas técnicas es que la construcción nos permite extender la estructura algebraica para varias familias de complejos simpliciales que se parecen mucho a las matroides. Esto nos deja trabajar en matroides con herramientas de combinatoria topológica y geométrica que está fuera del alcance de la teoría de matroides clásica. Presentaremos varias conjeturas para las clases nuevas se objetos. Esta charla es basada en trabajo conjunto con Federico Castillo y Jeremy Martin y servirá como motivación para la charla de Federico.
15.40-16.10
Federico Castillo (University of Kansas, USA)
Monoides de Hopf de matroides ordenadas
Continuando con el trabajo de M. Aguiar y F. Ardila sobre monoides de Hopf y matroides, construimos un monoide que considera matroides al tiempo que un orden lineal sobre el conjunto base. En el proceso de calcular la antipoda de este monoide por sorpresa nos encontramos complejos simpliciales combinatoricamente interesantes. La idea es mostrar como la teoria de combinatoria topologica nos puede ayudar a entender un objeto algebraico mucho mejor. Esta charla es basada en trabajo conjunto con Jeremy Martin y Jose Samper.