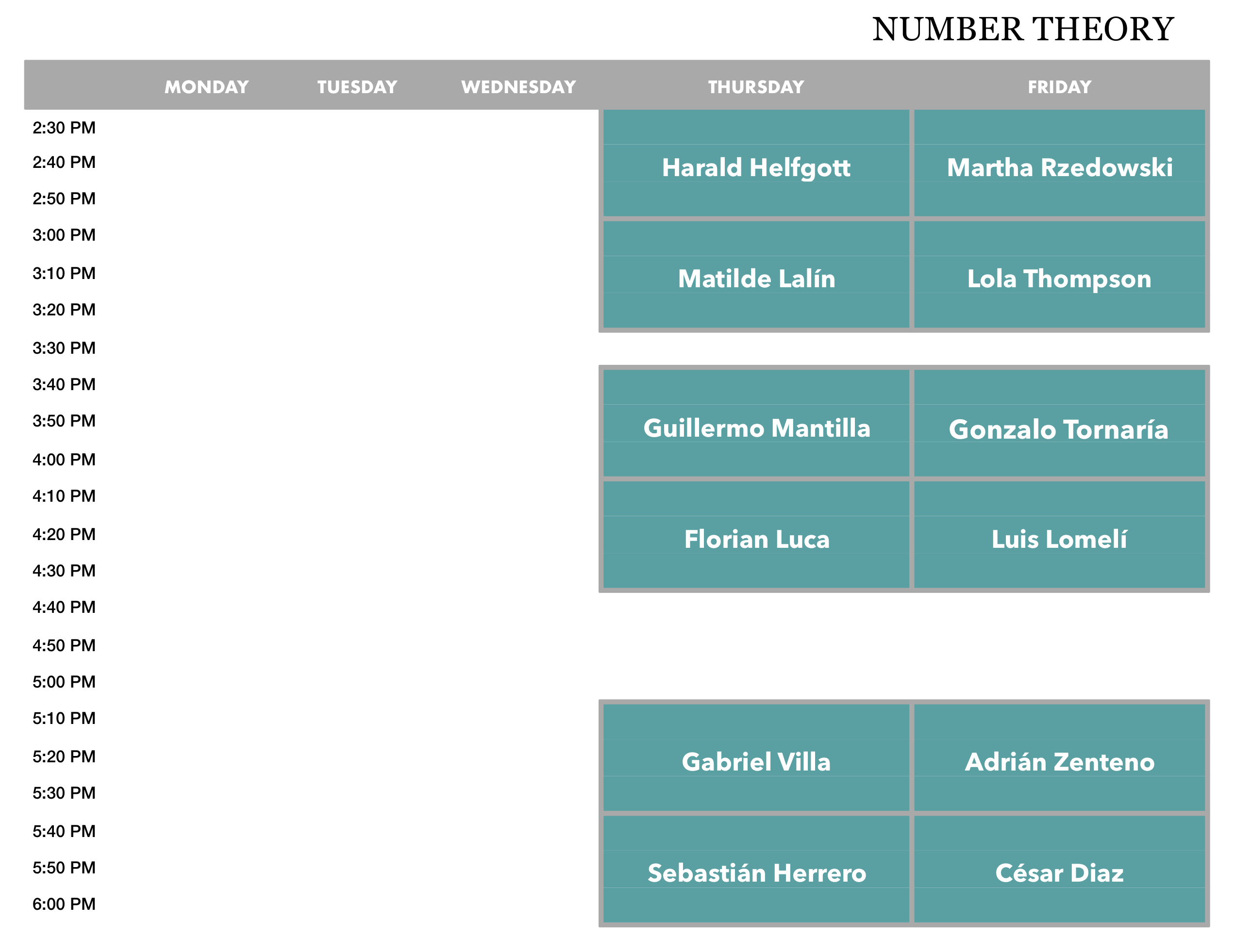
Session on Number Theory:
Thursday, August 8
14.30-14.55
Harald Helfgott (Universität Göttingen, Deutschland)
Cómo sumar $\mu(n)$: un mejor algoritmo elemental
Consideremos cualquiera de dos problemas relacionados: determinar el numero preciso $\pi(x)$ de números primos $p\leq x$, y calcular el valor $M(x)$ de la función de Mertens $M(x) = \sum_{n\leq x} \mu(n)$, donde $\mu$ es la función de Moebius.
Los dos mejores algoritmos conocidos son los siguientes:
1. Un algoritmo analítico (Lagarias-Odlyzko, 1987), con calculos basados sobre integrales o ceros de $\zeta(s)$; toma tiempo $O(x^{1/2+\epsilon})$.
2. Un algoritmo más elemental (Meissel-Lehmer, 1959 and Lagarias-Miller-Odlyzko, 1985; refinado por Deléglise-Rivat, 1996), que corre en tiempo $O(x^{2/3})$.
El algoritmo analítico fue implementado de manera rigurosa e incondicional por primera vez casi 30 años después de ser descrito (Platt, 2015), y sólo para $\pi(x)$; su implementación para $M(x)$ podría ser más difícil. Lo que es más, en el rango explorado hasta ahora ($x\leq 10^{24}$), el algoritmo elemental es más rápido en la práctica.
Presentaremos un algoritmo elemental e incondicional para calcular $M(x)$ que corre en tiempo aproximadamente $O(x^{3/5})$. El algoritmo debería poder adaptarse para calcular $\pi(x)$ y otras funciones relacionadas.
15.00-15.25
Matilde Lalín (Université de Montréal, Canada)
Conjectures for moments associated with cubic twists of elliptic curves
We extend the heuristic introduced by Conrey, Farmer, Keating, Rubinstein and Snaith in order to formulate conjectures for the $(k, \ell)$-moments of $L$-functions of elliptic curves twisted by cubic characters. We also apply the work of Keating and Snaith on the $(k,\ell)$-moments of characteristic polynomials of unitary matrices to extend our conjecture to $k, \ell \in \mathbb{R}_{>-1}$ such that $k+\ell\geq 0$. Our conjectures are then numerically tested for two families. This is joint work with C. David and J. B. Nam.
15.40-16.05
Guillermo Mantilla (Universidad Konrad Lorenz, Colombia)
On a question about Dedekind zeta functions and related results
Let $K$ be a number field. The $K$-arithmetic type of a rational prime $\ell$ is the tuple $A_{K}(\ell)=(f^{K}_{1},...,f^{K}_{g_{\ell}})$ of the residue degrees of $\ell$ in $K$, written in ascending order. A well known result of Perlis from the 70's states that two number fields have the same Dedekind zeta function if and only if for almost all primes $\ell$ the arithmetic types of $\ell$ in both fields coincide. By the end of the 90's Perlis and Stuart asked if having the same zeta function implies that for ramified primes the sum of the ramification degrees coincide. During the talk we will answer their question for a nontrivial and interesting class of cases. Moreover, using basic facts from the theory of Galois representations we will provide an alternative proof to the fact that the zeta function of $K$ is determined by the lengths of $K$-arithmetic types over the primes.
16.10-16.35
Florian Luca (University of the Witwatersrand, South Africa)
$X$ and $Y$-coordinates of Pell equations in various sequences
Let $d>1$ be a squarefree integer and $(X_n,Y_n)$ be the $n$th solution of the Pell equation $X^2-dY^2=\pm 1$. Given your favourite set of positive integers $U$, one can ask what can we say about those $d$ such that $X_n\in U$ for some $n$? Formulated in this way, the question has many solutions $d$ since one can always pick $u\in U$ and write $u^2\pm 1=dv^2$ with integers $d$ and $v$ such that $d$ is squarefree obtaining in this way that $(u,v)$ is a solution of the Pell equation corresponding to $d$. What about if we ask that $X_n\in U$ for at least two different $n$'s? Then the answer is very different. For example, if $U$ is the set of squares, then it is a classical result of Ljunggren that the only such $d$ is $1785$ for which both $X_1$ and $X_2$ are squares. In my talk, I will survey recent results about this problem when $U$ is the set of Fibonacci numbers, Tribonacci numbers, $k$-Generalized Fibonacci numbers, sums of two Fibonacci numbers, rep-digits (in base $10$ or any integer base $b\ge 2$), and factorials. We also present some results concerning the same problem for $Y$-coordinates. The proofs use linear forms in logarithms and computations and in the case of factorials results about primes in arithmetic progressions. These results have been obtained in joint work with various colleagues such as J. J. Bravo, C. A. Gómez, S. Laishram, A. Montejano, L. Szalay and A. Togbé and recent Ph.D. students M. Ddamulira, B. Faye and M. Sias.
17.10-17.35
Gabriel Villa (CINVESTAV, México)
Caracteres de Dirichlet y Campos de Géneros en Campos
El campo de géneros de un campo global de funciones $K$ con respecto a un subcampo $K_0$ es la parte sencilla del campo de clase de Hilbert $K_H$ de $K$. Más precisamente, el campo de géneros $K_{\mathfrak{ge}}$ de $K$ es $K_{\mathfrak{ge}}=KK_0^*$ donde $K_0^*$ es la máxima extensión abeliana de $K_0$ contenida en el campo de clase de Hilbert $K_H$ de $K$.
En esta plática pretenderemos describir como obtener $K_{\mathfrak{ge}}$ cuando $K/k$ es una extensión finita separable donde $k={{\mathbb F}_q}(T)$ es el campo de funciones racionales. Énfasis particular se hará en el caso en que $K/k$ es una extensión abeliana.
Nuestra herramienta principal es el uso del grupo de caracteres de Dirichlet asociado a un campo de funciones ciclotómico $K$. Usamos el análogo al estudo de la aritmética de los campos de funciones ciclotómicos hecha por Leopoldt en 1953 en campos numéricos. También se hace uso de la teoría de campos de clase, especialmente la global y particularmente la correspondientes a los campos de funciones.
17.40-18.05
Sebastián Herrero (Chalmers University, Sweden)
Solutions of equations involving the modular $j$ function
Inspired on Zilber's work on pseudo-exponentiation, in particular on his analysis of the complex exponential field, several authors have studied the existence of generic solutions of systems of exponential-polynomial equations. Results on the existence of solutions in certain cases follow from the work of Katzberg (1983) and Brownawell and Masser (2016), among others. On the other hand, assuming Schanuel's conjecture, Marker (2006), Mantova (2016) and D'Aquino, Fornasiero and Terzo (2018) have proved that generic solutions also exist (again, in certain cases). Since there are plenty of analogies between the exponential and the modular $j$ function, it is natural to ask if the results mentioned above can be replicated for the $j$ function. In this talk I will report on work in progress in collaboration with Sebastián Eterović (University of Oxford) where we prove that solutions of certain systems of polynomial equations involving the $j$ function exist. Moreover, assuming a modular analogue of Schanuel's conjecture, we obtain results on the existence of generic solutions.
Friday, August 9
14.30-14.55
Martha Rzedowski (CINVESTAV, México)
Campo de Géneros Extendido
La teoría de géneros se remonta a Gauss en el contexto de formas cuadráticas binarias. En la charla se presentan un bosquejo histórico del desarrollo de los conceptos campo de géneros y campo de géneros extendido y también algunos resultados tanto para campos numéricos como para campos de funciones con campo de constantes finito.
15.00-15.25
Lola Thompson (Oberlin College, USA)
Sumas de divisores
Sea $s(\cdot)$ la suma de divisores propios, en otras palabras, $s(n) = \sum_{d\mid n, \, d < n}d$. Esta función tiene una gran historia debido a su conexión con el estudio de los numeros perfectos. Erdos-Granville-Pomerance-Spiro conjeturaron que, para cualquier conjunto $\mathcal{A}$ de densidad asintótica zero, el conjunto $s^{-1}(\mathcal{A})$ también tiene densidad zero. Nosotros probamos una forma débil de esta conjectura. Esta charla está basada en trabajo conjunto con Paul Pollack y Carl Pomerance.
15.30-15.55
Gonzalo Tornaría (Universidad de La República, Uruguay)
TBA
16.10-16.35
Luis Lomelí (Pontificia Universidad Católica de Valparaíso, Chile)
${\rm SL}_*$ groups and the adeles
We prove that the ring of adeles over a global field is a $*$-Euclidean ring and study the ${\rm SL}_*$ groups of Pantoja and Soto-Andrade [PaSA2003]. The Bruhat decomposition allows us to connect to the Langlands-Shahidi local coefficient of $\mathfrak{p}$-adic representations and to automorphic representations [Sh1981], enabling Number Theoretic applications. We provide a proof of compatibility of Asai $L$-functions with the local Langlands correspondence for ${\rm GL}(2)$ based on a method of Henniart and Henniart-Lomelí [He2010, HeLo2013].
Referencias:
[He2010] G. Henniart, Correspondance de Langlands et fonctions $L$ des carrés extérieur et symétrique, Int. Math. Res. Not. (2010), no.4, 633-673.
[HeLo2013] G. Henniart and L. Lomelí, Characterization of $\gamma$-factors: the Asai case, Int. Math. Res. Not. (2013), no. 17, 4085-4099.
[PaSA2003] J. Pantoja and J. Soto-Andrade, A Bruhat decomposition of the group ${\rm SL}_*(2,A)$, J. Algebra 262 (2003), 401-412.
[Sh1981] F. Shahidi, On certain $L$-functions, Amer. J. Math. 103 (1981), 297-355.
17.10-17.35
Adrián Zenteno (Pontificia Universidad Católica de Valparaíso, Chile)
On the image of the Galois representations attached to Siegel modular forms
Let $G$ be a connected reductive group over $\mathbb{Q}$ and $^LG$ be the $L$-group of $G$. The (conjectural) global Langlands correspondence for $G$ predicts a correspondence between certain automorphic representations $\pi$ of $G(\mathbb{A}_{\mathbb{Q}})$ and certain $\ell$-adic Galois representations $\rho_{\pi,\ell} : \mbox{Gal}(\overline{\mathbb{Q}}/\mathbb{Q}) \longrightarrow {^{L}G}(\overline{\mathbb{Q}}_\ell)$. Some results of Serre (for elliptic curves), Ribet-Momose (for classical modular forms), Dieulefait (for Siegel modular forms of genus 2 and level 1) and Dieulefait-Vila (for cuspidal automorphic representations of GL(3) and GL(4)) suggest that the image of $\rho_{\pi,\ell}$ will be large for almost every prime if and only if $\pi$ is genuine to the group $G$, i.e., if $\pi$ does not come from an automorphic representation of a reductive group smaller than $G$.
In this talk I will explain how, by using Serre's modularity conjecture, Langlands functoriality and some recent results about residual irreducibility of compatible systems, we can prove that the i mage of the Galois representations attached to ``genuine'' cuspidal automorphic representations of $G=\mbox{GSp(4)}$ are as large as possible for almost every prime. Moreover, I will try to explain what is expected in general for GSp(2n). This is a joint work with Luis Dieulefait.
17.40-18.05
César Diaz (UNAM-UMSNH, México)
Productos de subconjuntos de pequeños intervalos y aplicaciones
Sean $p$ un número primo grande, $h>0$ y $s$ enteros, y $\mathcal{X}\subset [1,h]\cap \mathbb{Z}$. Siguiendo el trabajo de Bourgain, Garaev, Konyagin, y Shparlinski [BGKS-2], estudiaremos el problema de obtener cotas superiores no triviales para el número de soluciones a la congruencia $$\prod_{i=1}^{4}(x_i+s)\equiv \prod_{j=1}^{4}(y_j+s)\not \equiv 0 \pmod{p}, \quad x_i,y_j\in \mathcal{X}.$$ Veremos como una cota de este tipo se puede aplicar para obtener resultados acerca del número de puntos enteros sobre curvas exponenciales módulo un primo. Es un trabajo conjunto con Moubariz Garaev y José Hernández.
Referencia:
[BGKS-2] J. Bourgain, M. Z. Garaev, S. V. Konyagin, and I. E. Shparlinski, On congruences with products of variables from short intervals and applications, Proc. Steklov Inst. Math., 280} (2013) 61-90.